C语言实现仿射变换的加密解密

1 . 什么是仿射变换

在密码学中，仿射变换是一种加密技术，它是一种线性变换方法，用于对数据进行加密。这种加密方法基于数学公式和线性代数原理，通过将输入数据的每个元素与一个矩阵相乘，然后加上一个向量来转换数据。

仿射变换通常由两个主要部分组成：

  1. 线性变换：这一部分涉及将输入数据与一个固定的矩阵相乘。这个矩阵包含了加密算法的关键参数，也就是密钥的一部分。线性变换是仿射变换的核心部分，它用于混淆输入数据。
  2. 平移（或向量加法）：在线性变换之后，通常还会将一个向量（又称偏移向量）添加到结果中，以进一步混淆数据。这个向量也是密钥的一部分，用于增加加密的复杂性。

在数学上，仿射变换可以表示为：
$$
E(x)=Ax+B
$$
其中：

  • E(x) 是加密后的数据。
  • x 是输入数据。
  • A 是线性变换的矩阵。
  • B 是平移向量.

解密操作可以通过应用仿射变换的逆操作来完成。通常，如果 A 是可逆的（即它的逆矩阵存在），那么解密操作可以表示为：
$$
D(y)=A^{-1}(y−B)
$$
其中*D(y) 是解密后的数据，y 是加密后的数据。

仿射变换在密码学中常常用于块密码和流密码等加密算法中的不同阶段。虽然它是一种线性变换方法，但通过适当选择参数，可以提供一定的安全性，尤其在与其他复杂的加密技术结合使用时。然而，对于高级的密码需求，通常会使用更复杂的加密算法，如AES（高级加密标准）。

2. 代码实现

2.1 流程图👇

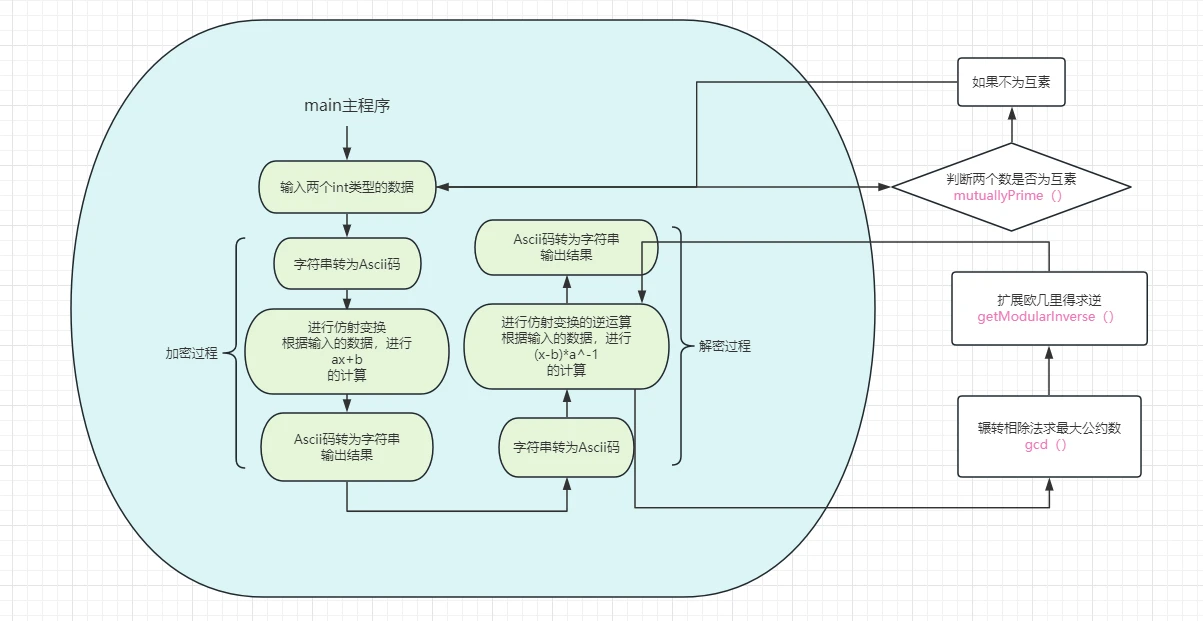
2.2 各个函数的功能，及实现

2.2.1 void compare(int &a, int &b)

​ 比较两个数字的大小，顺便把两个变量里面的值改为 第一个数最大，第二个数最小

1
2
3
4
5
6
7
8
9
10
void compare(int &a, int &b)
{
    if (b > a)
    {
        int tmp;
        tmp = b;
        b = a;
        a = tmp;
    }
}

2.2.2 bool mutuallyPrime(int a, int b)

​ 判断两个数字是否互素，如果互素，则返回True，否则返回False

​ 首先用compare函数判断两个数的大小，然后通过求余是否为1，判断是否互素

1
2
3
4
5
6
7
bool mutuallyPrime(int a, int b)
{
    bool flag = false;
    compare(a, b);
    if(a%b == 1) flag = true;
    return !flag;
}

2.2.3 int *string2Ascii(char str[])

​ 把字符数组转换为Ascii码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int *string2Ascii(char str[])
{
    int len = strlen(str);
    int *asciiValues = (int *)malloc(len * sizeof(int));
    if (asciiValues == NULL)
    {
        return NULL; // 如果内存分配失败，返回NULL
    }
    *(asciiValues + len) = -1;

    for (int i = 0; i < len; i++)
    {
        asciiValues[i] = (int)str[i];
    }

    return asciiValues;
}

2.2.4 char *affineTransformation(char str[], int a, int b)

​ 进行加密的仿射变换

  • 核心代码：

    1
    2
    3
    4
    5
    6
    7
    for (int i = 0; i < len; i++)
        {
            int num = *(p + i);
            if (num >= 'A' && num <= 'Z'){result[i] = (char)('A' + ((a * (num - 'A') + b)) % 26);}
            else if (num >= 'a' && num <= 'z'){result[i] = (char)('a' + ((a * (num - 'a') + b)) % 26);}
            else{result[i] = (char)num;}
        }

    根据输入的两个质数进行仿射变换

    • num - 'A' 字母转化为Ascii码后为65….等，需要减去a、A字符，转化为26之内的数字，方便做仿射变换

    • 'a' + ((a * (num - 'a') + b) 进行完仿射变换之后，需要把第一个字母加回来，目的是从Ascii码转为字符之后可以显示正常

  • 完整函数代码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    char *affineTransformation(char str[], int a, int b)
    {
        int *p = string2Ascii(str);
        int len = 0;

        // 计算输入字符串的长度
        while (*(p + len) != -1)
        {
            len++;
        }

        char *result = (char *)malloc((len + 1) * sizeof(char)); // +1 用于存储终止字符 '\0'

        for (int i = 0; i < len; i++)
        {
            int num = *(p + i);
            if (num >= 'A' && num <= 'Z')
            {
                result[i] = (char)('A' + ((a * (num - 'A') + b)) % 26);
            }
            else if (num >= 'a' && num <= 'z')
            {
                result[i] = (char)('a' + ((a * (num - 'a') + b)) % 26);
            }
            else
            {
                result[i] = (char)num;
            }
        }

        result[len] = '\0'; // 添加字符串终止字符

        return result;
    }

2.2.5 int *gcd(int a, int b, int *x, int *y)

转相除法求最大公约数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int gcd(int a, int b, int *x, int *y)
{
    if (a == 0)
    {
        *x = 0;
        *y = 1;
        return b;
    }

    int x1, y1;
    int gcd_val = gcd(b % a, a, &x1, &y1);

    *x = y1 - (b / a) * x1;
    *y = x1;

    return gcd_val;
}

2.2.6 int *getModularInverse(int num, int modNum)

求乘法逆元

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int getModularInverse(int num, int modNum)
{
    int x, y;
    int gcd_val = gcd(num, modNum, &x, &y);

    if (gcd_val != 1)
    {
        // 模逆不存在
        return -1;
    }
    else
    {
        // 确保结果在[0, m-1]范围内
        int result = (x % modNum + modNum) % modNum;
        return result;
    }
}

2.2.7 char *affineTransformationDecryption(char str[], int a, int b)

进行仿射变换的【解密】,接收到的a,b必须互素 ,str接收到加密的数据

  • 核心代码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    if (num >= 'A' && num <= 'Z')
            {
                int num_befor = (inverseElement * ((num - 'A') - b)) % 26;
                if (num_befor<0)
                {
                    num_befor += 26;
                }
                result[i] = (char)('A' + num_befor);
            }
            else if (num >= 'a' && num <= 'z')
            {
                int num_befor = (inverseElement * ((num - 'a') - b)) % 26;
                if (num_befor<0)
                {
                    num_befor += 26;
                }
                result[i] = (char)('a' + num_befor);
            }
            else
            {
                result[i] = (char)num;
            }
    • inverseElement * ((num - 'a') - b)进行解密inverseElement是a(mod26)的乘法逆元

  • 完整代码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    char *affineTransformationDecryption(char str[], int a, int b)
    {
        int inverseElement = getModularInverse(a, 26);
        int *p = string2Ascii(str);
        int len = 0;

        // 计算输入字符串的长度
        while (*(p + len) != -1)
        {
            len++;
        }
        char *result = (char *)malloc((len + 1) * sizeof(char)); // +1 用于存储终止字符 '\0'

        for (int i = 0; i < len; i++)
        {
            int num = *(p + i);
            if (num >= 'A' && num <= 'Z')
            {
                int num_befor = (inverseElement * ((num - 'A') - b)) % 26;
                if (num_befor<0)
                {
                    num_befor += 26;
                }
                result[i] = (char)('A' + num_befor);
            }
            else if (num >= 'a' && num <= 'z')
            {
                int num_befor = (inverseElement * ((num - 'a') - b)) % 26;
                if (num_befor<0)
                {
                    num_befor += 26;
                }
                result[i] = (char)('a' + num_befor);
            }
            else
            {
                result[i] = (char)num;
            }
        }

        result[len] = '\0'; // 添加字符串终止字符
        return result;
    }

3. 一些问题

3.1 为什么要a，b两个数互素？

在密码学中，要确保使用仿射变换是安全的，通常要求密钥中的参数 a 和 b 必须是互素的（也被称为互质或互不整除）。这是因为如果 a 和 b* 不是互素的，那么密钥将导致一些安全性问题：

  1. 周期性模式：如果 a 和b 不是互素的，那么加密函数
    $$
    E(x)=(ax+b)modm
    $$
    将导致周期性模式。这意味着在明文空间中的一些值可能会被映射到相同的密文值，这会降低密码系统的安全性，因为攻击者可以通过分析频率和统计信息来破解密码。

  2. 可逆性问题：如果 a 和 b 不是互素的，那么解密函数
    $$
    D(y)=a
    −1
    (y−b)modm
    $$
    中的 a^-1（a 的模 m 乘法逆元）可能不存在。在这种情况下，加密操作是可逆的，但解密操作无法正确执行，导致密码无法正常工作。

确保 a* 和 b* 互素是为了避免这些问题。互素的 a* 和 b* 意味着它们没有共同的因子，除了1以外没有其他公共的正整数因子。这样可以确保加密和解密操作在数学上是可逆的，不会引入不必要的周期性或可预测性。因此，互素的 a* 和 b* 是安全性的一个关键要求，以保护密码系统免受攻击。